複利計算の仕組みを理解していますか。
お金の勉強をしていると必ずと言っていいほど登場するのがこの言葉です。
ところが数式や%が登場するので苦手意識をお持ちの方もいる事でしょう。
そこで今回は複利について一切数式を使わずにお話していきます。
人類にとって最大の発明
かの天才科学者アインシュタインは
「複利は人類にとって最大の発明だ 知っている者は複利で稼ぎ 知らない者は複利を払う」
と言ったとされています。
これは決して大げさではなく、少しの利益が時間と共に雪だるま式に膨らむ複利の力を称賛した言葉です。
10年、20年と積み重ねることで、最初の投資額は何倍にもなっていきます。
アインシュタインがこの力を「最も強力」と言ったのは、それだけ人々の生活を大きく変え得る、素晴らしい可能性を秘めているからです。
複利計算についてはお金の世界でよく話題になります。
ただ、一般的に数式を用いて説明されたり、利率や%など耳馴染みのない言葉も多く登場します。
そのため、苦手意識をお持ちの方もいらっしゃるのではないでしょうか。
そこでここではあえて一切数式を使わずに、日常生活になぞらえてイメージをしていただきます。
出勤にかかる時間
同じビルの同じフロアにある会社に勤めているAさんとBさんがいました。
たまたまこのAさんとBさんは同じ高層マンションの最上階に住むお隣さん同士です。
この2人の通勤時間について考えてみましょう。
Aさんは7時30分に家を出てエレベーターに乗り1階におります。
マンションの前の信号がタイミングよく青になったので、スムーズに地下鉄駅に到着します。
ホームにおりてすぐに到着した7時40分発の地下鉄に乗って、会社に出勤したのが8時00分です。
一方のBさんは7時31分に家をでました。
このBさんが会社に到着するのは何時何分でしょう。
家を出た時のAさんとの差は1分だから8時1分に出勤できるでしょうか。
普段の生活をイメージしながら考えてみてください。
Bさんが家を出て乗ろうとしたエレベーターは既にAさんが乗って1階に向かっています。
そのためBさんはエレベーターに乗るまでに待ち時間が3分発生します。
無事に1階におりたBさんですが、残念ながら信号待ちにかかってしまいここでも3分待ちます。
地下鉄駅に到着したのは7時47分ですが、次の地下鉄が発車するのは7時51分です。
地下鉄待ちで4分の時間が余分にかかってしまいました。
結果的にBさんが出勤したのは8時11分でした。
Aさんと比べて10分遅く会社に到着です。

複利を味方にするか敵にするか
先ほどの例では、家を出た時間は僅か1分しか変わりませんでした。
ところが、エレベーター、信号、地下鉄によって待ち時間が発生したことによって最終的な到着時間は10分も遅くなってしまいました。
最初の1分間の遅れが後の遅れを引き起こしたということですね。
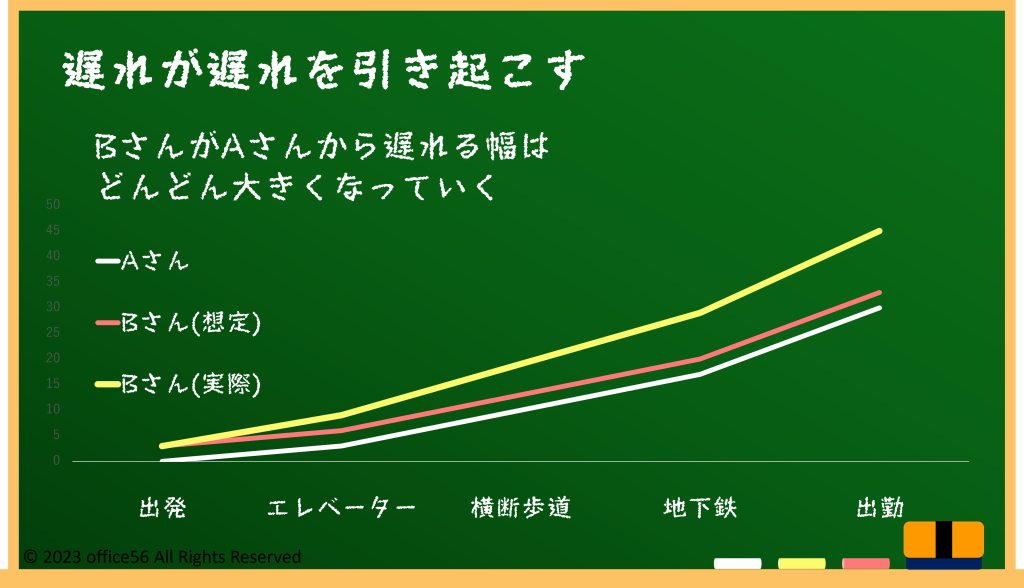
この遅れた時間を資産、エレベーターや地下鉄を利用する回数を時間と置き換えて考えてみます。
期間が長ければ長いほどお金が増える幅が大きくなるイメージがつくでしょうか。
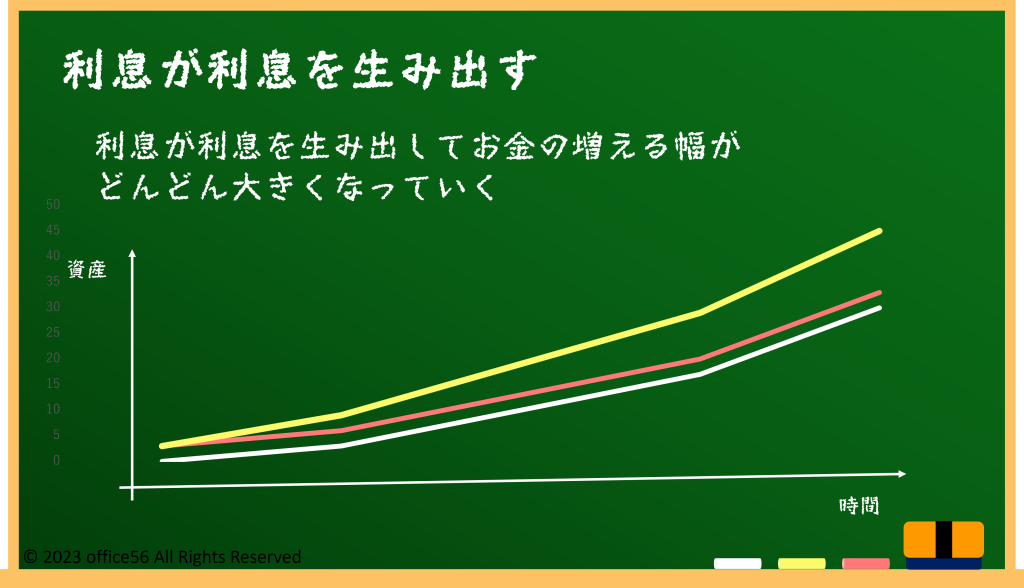
複利計算も同じようなイメージです。
時間が経てば経つほどその効果は大きくなります。
複利を味方につけるか、敵に回すか、これは重要なポイントです。
例えば、少額でも投資をはじめて複利を味方にすることで、じわじわと資産を増やすことができます。
小さなもったいない支出の見直しも、その後の長い人生で大きな効果になります。
しかし一方で注意が必要なのは、高金利の借金です。これがあると、複利が逆に敵に回ります。
クレジットカードの残高をそのままにしておくと、利息が膨らんでしまう…これも複利の力です。
ちょっと怖いですね。
まとめ
複利は期間が長ければ長いほどプラスにもマイナスにも大きく作用します。
自分の生活に複利をどう取り入れ、どう避けるかが大切です。
僅かな差だと甘く見ずに、小さなお得や少しのもったいない削減をコツコツと積み上げていきましょう。
それは将来きっとあなたにとって大きな助けになるはずです。
